Rahmstorf extrapolates out more than five times the measured temperature domain

This is part of a series of posts concerning Problems with the Rahmstorf (2007) paper.

Critique #3. Rahmstorf extrapolates out more than five times the measured temperature domain.

Extrapolation is risky business. Even when the fitted model accurately describes the real data over its domain, extrapolation beyond that domain can lead to very poor predictions. When the fitted model does not accurately describe the measured data (Rahmstorf's unbinned sea level rise rate vs. temperature, see figure 3, here, for example) the result can be truly bizarre. The NIST Engineering Handbook states:

Modeling and prediction allows us to go beyond the data to gain additional insights, but they must be done with great caution. Interpolation is generally safer than extrapolation, but mis-prediction, error, and misinterpretation are liable to occur in either case...The best attitude, and especially for extrapolation, is that the derived conclusions must be viewed with extra caution. !

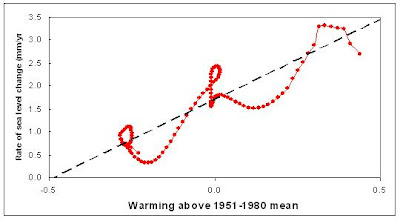
Rahmstorf's projection for future sea level (figure 4 in his paper), is reproduced in part in figure 1, below, and makes it look as if his measurement domain is 120 years and that he has extrapolated out another 100 years. But in reality, his measurement domain was in decrees C of temperature anomaly, and his range was in sea level rise rate. Extrapolating out 100 years based on 120 years of data would be bad enough, but he actually extrapolates out more that 5
°C based on 0.8 °C of data. See figure 2! This is an extrapolation of poorly fit data to over six time the measured data domain!!!

Figure 1. Reproduction of Rahmstorf's figure 4, showing "sea-level projections
from 1990 to 2100." This image gives the impression that it shows an extrapolation from measured sea level data spanning 120 years out for an additional 100 years.

Figure 2. But the real extrapolation is from the sea level rise vs temperature plot. First he fits a straight line to a twisted piece of spaghetti, then extends that line way, way out.

This type extreme form of extrapolation is best summed up by Mark Twain in Life on the Mississippi (1883). Twain writes about effect of cutting across "horseshoe curves" in the river over the years in order to shorten it.

" The Mississippi between Cairo and New Orleans was twelve hundred and fifteen miles long one hundred and seventy-six years ago. It was eleven hundred and eighty after the cut-off of 1722. It was one thousand and forty after the American Bend cut-off. It has lost sixty-seven miles since. Consequently its length is only nine hundred and seventy-three miles at present.

Now, if I wanted to be one of those ponderous scientific people, and `let on' to prove what had occurred in the remote past by what had occurred in a given time in the recent past, or what will occur in the far future by what has occurred in late years, what an opportunity is here! Geology never had such a chance, nor such exact data to argue from! Nor `development of species', either! Glacial epochs are great things, but they are vague--vague. Please observe. In the space of one hundred and seventy-six years the Lower Mississippi has shortened itself two hundred and forty two miles. This is an average of a trifle over one mile and a third per year. Therefore, any calm person, who is not blind or idiotic, can see that in the Old Oolitic Silurian Period, just a million years ago next November, the Lower Mississippi River was upward of one million three hundred thousand miles long, and stuck out over the Gulf of Mexico like a fishing-rod. And by the same token any person can see that seven hundred and forty-two years from now the Lower Mississippi will be only a mile and three-quarters long, and Cairo and New Orleans will have joined their streets together, and be plodding comfortably along under a single mayor and a mutual board of aldermen. There is something fascinating about science. One gets such wholesale returns of conjecture out of such a trifling investment of fact."

Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

1. Rahmstorf, A Semi-Empirical Approach to Projecting Sea Level Rise, Science 315, 368 (2007)

Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

Time for sea level to reach equilibrium is not millennia

This is part of a series of posts concerning Problems with the Rahmstorf (2007) paper.

Critique #2. The assumption that the time required to arrive at the new equilibrium is "on the order of millennia" is not borne out by the data.

This assumption implies that on a century time scale a temperature rise will result in an increase of the sea level rise rate, and the sea level rise rate will not drop back down unless there is a significant drop in the temperature, as illustrated in figure 1, below.

Figure 1. Illustration of a Rahmstorf type model with a temperature step vs. time, the resulting step in the sea level rise rate (dH/dt) vs. time, and the combination of sea level rise rate vs. temperature. This scenario works under the assumption that the adjustment timescale for the sea level rise rate is on the order of millennia.

If the adjustment time were decades instead of millennia, then a temperature step would result in an increase of the sea level rise rate, quickly followed by a drop. This scenario is shown in figure 2, below.

Figure 2. Illustration of a short adjustment time model. As in figure 1, above, it shows a temperature step vs. time, the resulting step in the sea level rise rate (dH/dt) vs. time, and the combination of sea level rise rate vs. temperature.

The actual temperature (GISS) and sea level data (Church, 2006) is not as clean as the simple models illustrated in figures 1 and 2. However, the best example of a simple temperature step occurs between the years 1890 and 1970. Using the 15 year smoothed temperature ( deviation from the 1951 to 1980 average) and sea level rise data it can be seen that from about 1890 to about 1915 the temperature was quite steady (-0.265 ºC ± 0.015 ºC), followed by a rapid rise of about 0.25 ºC by 1940. Then from 1940 to the mid 70s the temperature stays about 0.0 ºC ± 0.015 ºC.

What does the sea level rise rate do during this same period? When the temperature is flat from 1890 to 1915 the sea level rise rate is dropping. As the temperature rises until 1940, the sea level rise rate also rises. Shortly after that the sea level rise rate stars dropping while the temperature remains flat again. Figure 3, below, shows the temperature and sea level rise rate during this interesting time period.

Figure 3. Temperature anomaly and sea level rise rate from 1890 to 1970. Same data that Rahmsdorf used, 15 year smoothing.

According to Rahmstorf's model the sea level rise rate should have been constant during the periods when the temperature was constant. The fact that the sea level rise rate was dropping during both of these periods indicates that the adjustment time is not on the order of millennia, but rather on the order of decades. This has a profound impact on his conclusions. According to Rahmstorf's model, a temperature rise that occurs in the early 1900s would still be contributing to sea level rise in 2100. The data indicates otherwise: the effect of a temperature step on sea level rise diminishes in only decades.

Figure 4. Rahmstorf's and Moriarty's smoothed and binned sea level rise rate vs. temperature anomaly, Moriarty's unbinned version, and Moriarty's unbinned version with the data from figure 3, above, highlighted showing regions of constant temperature and decreasing sea level rise rate.

Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

1. GISS: http://data.giss.nasa.gov/gistemp/

2. J. A. Church, N. J. White, Geophys. Res. Lett. 33, L01602 (2006).
3. Rahmstorf, A Semi-Empirical Approach to Projecting Sea Level Rise, Science 315, 368 (2007)


Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

Rahmstorf's sea level rise rate vs. T does not fit a line

This is part of a series of posts concerning Problems with the Rahmstorf (2007) paper.

Critique #1. Sea level rise rate vs. temperature is displayed in a way that erroneously implies that it is well fit to a line.

Rahmstorf's figure 2 shows the sea level rise rate vs. temperature in the form of 24 discreet points. These points are derived by binning the 120 points that represent each individual year from 1880 to 2000 into groups of 5 after smoothing the sea level data (Church, 2006) and temperature data (GISS) with with a nonlinear trend technique. My digitized version of his plot is shown in figure 1, below.

Figure 1. Rahmstorf's version of sea level rise rate (mm/year) vs. temperature anomaly.

I smoothed the same sea level data and temperature data with a 15 year FWHM Gaussian filter. Note that the difference between smoothing the sea level data with the nonlinear trend line technique and with the Gaussian filter is vanishingly small, as demonstrated by the fact that I derived the same sea level rise rate vs. temperature as Rahmstorf does (sea level =3.375 *(T anomaly + 1.684, r = 0.86). My plot of sea level rise rate vs. temperature anomaly, which is very similar to Rahmstorf's, is shown below in figure 2. One might plausibly argue that the points in figures 1 and 2 could be reasonably fit to a line. That is precisely the argument that Rahmstorf makes.

Figure 2. Moriarty's version of sea level rise rate vs. temperature anomaly.

However, if the data is not binned, that is, all 120 data points are shown, then it becomes perfectly clear that fitting this data to a line is entirely inappropriate. Figure 3, below, shows the same data as figure 2, without binning.

Figure 3. When the sea level rise rate vs temperature anomaly data is not binned it appears that fitting it to a line is entirely inappropriate.

Rahmstorf seems to justify fitting this very non-linear data to a line by saying "A highly significant correlation of global temperature and the rate of sea-level rise is found (r = 0.88, P = 1.6 × 10−8) (Fig. 2) with a slope of a = 3.4 mm/year per °C." It should be understood that this is very poor justification. Section 4.4.4 of the The National Institute of Standards and Technology (NIST) Engineering Statistics Handbook says:

Model validation is possibly the most important step in the model building sequence. It is also one of the most overlooked. Often the validation of a model seems to consist of nothing more than quoting the R^2 statistic from the fit (which measures the fraction of the total variability in the response that is accounted for by the model). Unfortunately, a high R^2 value does not guarantee that the model fits the data well. Use of a model that does not fit the data well cannot provide good answers to the underlying engineering or scientific questions under investigation.

Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

1. GISS: http://data.giss.nasa.gov/gistemp/
2. J. A. Church, N. J. White, Geophys. Res. Lett. 33, L01602 (2006).
3. Rahmstorf, A Semi-Empirical Approach to Projecting Sea Level Rise, Science 315, 368 (2007)

Back to series of posts concerning Problems with the Rahmstorf (2007) paper.

Critique of "A Semi-Empirical Approach to Projecting Future Sea-Level Rise" by Rahmstorf

A recent article in Science by Stefan Rahmstorf (2007) predicted extreme sea level rise during the 21st century. Rahmstorf's predictions went as high as 140 cm (55 inches), far beyond even the high edge of the uncertainty of the IPCC's unlikely A1Fl scenario (see here, page 820). This high estimate by the IPCC was 59cm (23 inches), with other other scenarios yielding considerably lower estimates. Following is a critique of Rahmstorf's method and conclusions.

This post has a quick summary of Rahmstorf's approach to to projecting sea-level rise for this century. Following that summary is a quick list of problems that I have identified in his paper, each with a link to subsequent posts with more detailed information.


Rahmstorf's Simple Model


Rahmstorf's simple model of sea level rise consists of a system in equilibrium, where the sea level and the temperature start out as constants. Then an instantaneous step occurs in the temperature, causing the sea level to rise. Eventually the sea level will rise to a new equilibrium, as shown below.

It is very important to note that the time required to arrive at the new equilibrium is, according to Rahmstorf, "to be on the order of millennia." This long time scale provides the other important point of this simple model. That is, over a short enough time scale the rate of sea level rise can be considered a constant (as illustrated in the above graph during the time where dH/dT is proportional to delta T). Rahmstorf posits that "this linear approximation may be valid for a few centuries."

Therefore, in this model, a temperature jump in the 1920s, for example, would result in a sea level rising at a constant rate for several hundred years, even without any subsequent temperature increases. Of course, subsequent temperature rises would each result in a greater sea level rise rate, but there would never be any drop in the rise rate for several hundred years, assuming no significant drops in the temperature. The following section puts this model on a mathematical footing.

Rahmstorf's Mathematical Strategy

1) Assume that the rate of sea level rise rate at any given time is proportional to the deviation form some global equilibrium temperature at that time. He expresses this in the following formula...

where H is the sea level, dH/dt is the sea level rise rate, T is the temperature, To is the the equilibrium temperature, and a is the constant of proportionality.

2) To and a can be derived by simply plotting dH/dt vs T and fitting to a line.

3) Once To and a have been determined, then the sea level for any given time, H(t), can be calculated by integrating equation (I), above, with respect to time...

4) By applying various temperature rise scenarios for the 21st century to equation (II), Rahmstorf predicts the sea level for the hear 2100 (H(2100)).


Problems with this model

1) Sea level rise rate vs. temperature is displayed in a way that erroneously implies that it is well fit to a line, as expressed in equation I, above. More...

2) The assumption that the time required to arrive at the new equilibrium is "on the order or millennia" is not borne out by the data. More...

3)Rahmstorf extrapolates out more than five times the measured temperature domain. More...